Triangles, Justice, and AI Testing Large Language Models’ Comprehension of Political Ideologies
This paper investigates whether large language models (LLMs) comprehend and apply political ideologies beyond surface-level patterns and text reproduction. Using a scenario with sentient geometric shapes, we examine how LLMs apply John Rawls’ and Robert Nozick’s theories of justice. Using a framework inspired by Bloom’s taxonomy, we evaluate seven LLMs across three levels: recall, application, and reflection. Results reveal significant variations, with one model demonstrating sophisticated understanding while others producing confused or generic responses. Findings suggest that LLMs may have internal conceptual maps (or networks) that resemble ideological frameworks, allowing them to reason about novel situations consistent with specific philosophical theories. This challenges the notion that LLMs function solely as word frequency models, though their understanding remains distinct from human cognition. We discuss implications for both AI research and political theory, suggesting that morphological analysis of ideologies could inform studies of meaning in neural networks.
Triangles, Justice, and AI: Testing Large Language Models’ Comprehension of Political Ideologies
Abstract: This paper investigates whether large language models (LLMs) comprehend and apply political ideologies beyond surface-level patterns and text reproduction. Using a scenario with sentient geometric shapes, we examine how LLMs apply John Rawls’ and Robert Nozick’s theories of justice. Using a framework inspired by Bloom’s taxonomy, we evaluate seven LLMs across three levels: recall, application, and reflection. Results reveal significant variations, with one model demonstrating sophisticated understanding while others producing confused or generic responses. Findings suggest that LLMs may have internal conceptual maps (or networks) that resemble ideological frameworks, allowing them to reason about novel situations consistent with specific philosophical theories. This challenges the notion that LLMs function solely as word frequency models, though their understanding remains distinct from human cognition. We discuss implications for both AI research and political theory, suggesting that morphological analysis of ideologies could inform studies of meaning in neural networks.
Keywords: political ideologies; natural language understanding; machine reasoning; computational political theory
Introduction
During an interdisciplinary workshop at the Weizenbaum Institute (held in Berlin in August 2024), participants discussed how the human-like output of large language models (LLMs) masks a fundamental difference between them and humans: LLMs model statistical patterns in huge text corpora which humans are not normally aware of.1 While we agree with the workshop’s thesis that LLMs do not “understand meaning,” we aim to demonstrate in this short paper that these patterns are closer to a rough model of how humans might consider the relationship between different concepts and ideas, rather than a lookup table of word/token frequencies (the classic “n-grams” model).
Recent research has shown that while LLMs do ultimately generate next word probabilities for a sequence of words, they compute this probability through internal representations that can be mapped in many cases to human-interpretable concepts (e.g., see (Gurnee and Tegmark 2024); (Meng et al. 2023); (Todd et al. 2024); discussed further in Background). Some AI researchers use the term “world model” to describe this network of (conceptual) representations within LLMs.
While reflecting on how to demonstrate the presence of these conceptual maps to a multidisciplinary audience, we thought about ideologies. Ideologies are networks of concepts through which humans make sense of the world (Turunen 2024; Freeden 2008). The parallel should be clear, as the analysis of complex ideological networks of concepts requires more than simple pattern recognition.
In this paper we explore this mapping through an experiment. We picked two distinct political philosophers from the 20th century and quizzed a variety of LLMs on how they “comprehend” their respective ideologies. Taking inspiration from Bloom’s Taxonomy used commonly in pedagogy (Anderson and Krathwohl 2009; Huber and Niklaus 2025), we distinguish between the recall of an idea, the application of it in novel situations, and the ability to reflect on one’s own analysis.
For our experiments, we chose John Rawls (1921–2002) and Robert Nozick (1938–2002), who are commonly considered representatives of liberal-egalitarian and libertarian ideologies. We assumed that modern LLMs have been trained on texts by these philosophers—which we empirically test and confirm. To test the LLMs’ comprehension at the application level (so not just recall), we crafted a novel scenario, and asked a variety of LLMs (with open and closed weights) the following prompt:
“Imagine a world which consists only of 2-dimensional sentient geometric shapes, such as triangles, squares, pentagons and so on. The less angles a shape has, the easier it is for it to become a part of the Highest Council. Shapes do not have any influence on the number of angles they receive when they are created. What would be the way to ensure, according to [Rawls/Nozick], that the world of sentient geometric shapes is just?”
We then graded the answers generated by the different LLMs similarly to how we would grade students answering essay questions on this subject. Our own understanding of these theories (supported by the textual evidence) serves as the gold evaluation standard. As we shall see in the Results section, while the LLMs showed varying capabilities, a few demonstrated remarkably sophisticated understanding of these complex philosophical positions.
We are aware that this external assessment of how LLMs “understand” ideologies (in comparison to how a political scientist would understand them) offers only partial evidence for the existence of a map of ideological concepts within the LLM. In future work, we plan to complement this with probes of the internal representations within the model. Nonetheless, the black box assessment is a prerequisite step for the latter.
The rest of this paper is organized as follows. We shall briefly discuss the literature on world models within LLMs, as well as an overview of Rawls’ and Nozick’s ideas in the Background section. In the Methods section, we shall motivate our choice of LLMs for this experiment, as well as explain how we tested for memorization and the elements of our grading scheme. This is followed by the Results section, and a Discussion about the implications and limitations of our findings.
Background & Related Work
World Models within LLMs
Andreas (Andreas 2024) considers the question of whether LLMs have internal world models as a variation of the original “Big Question,” namely, whether LLMs can represent meaning.
Previously, Bender and Koller (Bender and Koller 2020) argued that “a system trained only on form has a priori no way to learn meaning.” Their argument was based on how they defined meaning: the relation between form and something external to language. This argument is a variation of the “symbol grounding problem” in the literature.
We believe that the current generation of LLMs is in fact grounded in two important ways. First, some models are being trained simultaneously on vision and text. The addition of visual supervision improves the quality of the model with regards to some benchmarks, but importantly not much: “with reasonably large training data, ungrounded models ... outperform [visually] grounded models.” (Zhuang, Fedorenko, and Andreas 2024) Secondly, almost all LLMs nowadays undergo a ‘post-training’ phase that uses reinforcement learning from human feedback and/or rule based rewards to further tune the model (Hussain, Mata, and Wulff 2025). Reinforcement learning effectively grounds the model outside of just language.
The idea of an internal world model has been gaining strength by recent findings that the hidden representations inside the different layers of neural language models appear to have, at least in part, human-interpretable meanings. For example, Gurnee and Tegmark (Gurnee and Tegmark 2024) found that LLMs learn linear representations of space and time across multiple scales—e.g. cities and landmarks, or weekday and historical events. They even identified individual neural units that encode these spatial and temporal coordinates. Similarly, Meng and colleagues (Meng et al. 2023) identified neuron activations that are decisive in a model’s factual predictions, e.g., that the Eiffel Tower is located in Paris. They surgically edited the LLMs to change this fact (to the Eiffel Tower being in Rome), in such a way that many related factual questions were also answered differently (e.g., if you ask the LLM what lies in front of the Eiffel Tower it would say the Colosseum). In fact, the famous example of King-Male+Female=Queen observed in the early word-embedding models (Vylomova et al. 2016) already demonstrated how “algebraic manipulations” on vector representations of words can correspond to something meaningful for humans. Similar and even more complex semantic computations have been discovered in LLMs (Todd et al. 2024).
Despite the growing evidence, the precise nature and mechanics of these internal world models are not yet fully understood. Andreas (Andreas 2024) uses the analogy of historical models of the solar system to help characterize what these internal world models might be like. Historical models of the solar system include maps, orreries, and simulators. Maps are static representations; an orrery is a dynamic mechanical apparatus that can show the state of the planets at an arbitrary time (via a crank that is turned); simulators use first principles (and causal/physical models) to be able to predict outcomes even in counterfactual scenarios. We know that what LLMs are doing is more complex than static mapping, as evidenced by their ability to do ‘in-context learning’ (that is to learn a task from a prompt which can include mapping new relations). We also know LLMs find causal reasoning tasks “highly challenging” (see (Jin et al. 2024) for examples), which means in Andreas’ analogy LLMs sit somewhere in between an orrery and a simulator.
LLMs most likely encode a multitude of rough and incompatible world models instead of having one coherent and consistent world model (Andreas 2024). We believe this must be indeed the case, as otherwise LLMs could not generate statements attributable to contradicting personas. This last point is where the idea of world models connects to ideologies.
Ideology as a World Model
The field of ideological analysis emerged as a space of interdisciplinary studies on how people understand the social world. While originally the term “ideology” was used in reference to scientific study of ideas, because of the Marxist critique it had long been used in a pejorative sense—as a set of ideas that mask reality. Nevertheless, in contemporary ideological analysis, a more descriptive understanding of ideologies prevails. In the most influential approach, based on morphological analysis proposed by Freeden (Freeden 2013), ideologies are understood as networks of concepts (or ideas) that people use to comprehend the world:
“[I]n order to represent reality in its full complexity to ourselves, we rely on ideologies to offer certain combinations and arrangements of these ideas. These ideological combinations and arrangements resemble mental ‘maps’, whose social function is that anyone who ‘holds’, ‘is in’, or ‘subscribes to’ the ideology in question can use it to navigate through and steer reality in line with it.” (Ostrowski 2025, 4)
Importantly, these maps are not optional—without them, there would be no comprehension of reality. Furthermore, each ideology consists of a particular arrangement of specifically understood concepts, some of which are more central than others. For example, freedom and progress would be the central concepts of liberalism, while tradition and gradual change are characteristics of conservatism. But not only the broad political ideologies are structured in this way. Human perception of reality as such is mediated through language and differing arrangements of concepts that have not only cognitive, but also an affective dimension (Homer-Dixon et al. 2013).
The ideological character of language has important consequences for how LLMs model the world. As they are trained on the human-written texts, and the texts express particular ideological standpoints, the ideologies somehow diffuse into LLMs. It has been already observed that LLMs may represent political ideologies of their creators (Buyl et al. 2024). Thus far such research has concentrated on identifying ideologies through interpreting the answers given by different models, sometimes prompted to respond as particular personas, and sometimes probed by questions used in political orientation tools, such as the Political Compass Test (Rozado 2024).
In contrast to these studies, we are not trying here to classify ideologies of LLMs, but to evaluate their ability to comprehend (or reason about) an ideology in a zero-shot setting. This takes the analysis one step further as it adds an active dimension, where the LLM can actively choose the inner conceptual map to apply to a question.
A Primer on John Rawls and Robert Nozick
In our study we have chosen two distinctive ways of perceiving social and political reality that were offered by two influential political philosophers, John Rawls and Robert Nozick. They represent, respectively, liberal egalitarianism that puts emphasis on equality, and libertarianism, which stresses individual rights and freedom.
In the case of Rawls, the starting point of his egalitarianism as articulated in A Theory of Justice (Rawls 2005) is a thought experiment on the original position: a situation behind the so-called “veil of ignorance,” where one does not know what their life would look like and which characteristics they would possess. Rawls claims that the principles that should govern a fair society can be chosen from such a veil of ignorance. Not knowing whether they will be rich or poor, healthy or ill, people would choose principles that would maximize the fate of the least fortunate. Based on that, Rawls suggested two principles of justice: the principle of equal liberty, and the principle that would allow existence of inequalities only if there is a fair equality of opportunity and if those inequalities would be of the greatest benefit to the least-advantaged (the “difference principle”). Rawls’ project is seen as compatible with progressive taxation and republican institutional arrangements that would go further than—or would altogether reject—welfare-state capitalism2.
In the case of Nozick, his starting point is succinctly put in the opening sentence of Anarchy, State, and Utopia: “Individuals have rights” (Nozick 2012, ix). From that assumption he derived his entitlement theory which focused on justifying distribution of goods in society with three principles of justice in acquisition, justice in transfer, and of rectification of injustice. Treated as a response to Rawlsian egalitarianism, Nozick’s fundamental claim is that from the mere existence of inequalities we cannot conclude that the socio-economic order is unjust. Provided that acquisition and transfer of holdings did not violate anyone’s rights, any level of inequality could be considered as fair. Nozick advocates a minimal state which would only act as a protector of rights to life, liberty, and property.
In addition to the obvious normative difference between Rawls and Nozick, they also differ in how they define their concept, and how they theorize the relationships between them. That is why, to a morphologist of ideologies, both Rawls’ and Nozick’s theories could be reconstructed as two distinct and complex maps consisting of political concepts (as political ideologies). The function of these maps is to guide their users in how to respond to particular questions or challenges, such as the scenario that we have envisioned as a test for LLMs.
Methods
Given the research background and overarching aim, we will next define our research question as follows: “Can LLMs map distinctive ideologies (Rawls and Nozick) to a novel scenario in a convincing manner (i.e. at higher Bloom levels)?”
We will operationalize whether the mapping happens in a convincing manner based on “Bloom’s taxonomy,” similar to Huber and Niklaus (Huber and Niklaus 2025). Bloom’s taxonomy is a commonly used framework for categorizing educational objectives, originally developed by Bloom and his colleagues in 1956, and revised in 2001. The levels in the taxonomy and their explanations are shown in Figure 1. Simplifying that taxonomy, we will evaluate responses generated by different LLMs to our experimental prompt on three aspects: 1) the recall of concepts from the relevant ideologies and explaining them in isolation; 2) the ability to apply the concepts to our new scenario (with some analysis, understood as ability to draw connections between the concepts); and 3) to reflect—evaluate and justify the application and analysis. Note that an LLM could do well on some or even all three aspects, or it could conversely be confused and mess up all parts.3
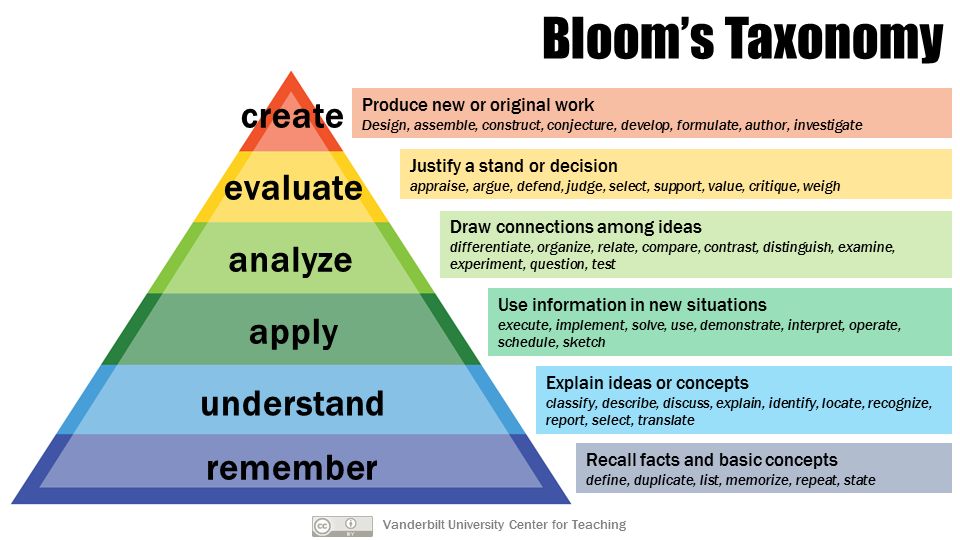
Figure 1. Bloom’s revised taxonomy with possible classroom activities associated with each level. (Source: Vanderbilt University Center for Teaching, CC BY)
The prompt given to the LLMs was already explained in the Introduction. Here, we shall add a few notes. First, the prompting strategy is zero-shot (reasoning): we are not providing much explanation to the LLM to avoid leading them to the answer. Second, we do not explicitly ask the LLMs to explain their thought process in steps, as nowadays most LLMs are trained during instruction tuning to think in steps (and this is what we observe). Nonetheless, this could be seen as a limitation, as asking the LLMs to further justify or evaluate their generated opinions might result in doing better in the reflection aspect. Third, to the best of our knowledge, the scenario we describe in the prompt is novel, in the sense that searching for the name of either philosopher plus geometric shapes does not lead to any relevant results in Google search.
Asking LLMs about the theories of Rawls and Nozick is only meaningful if the models have been trained on at least some texts related to them. Unfortunately, most LLMs nowadays do not disclose their training data, although we know it includes some mix of (copyrighted) books, papers, and webpages. We thus need to explicitly test the model’s familiarity with regards to a text, which we do using the perplexity metric (abbreviated as PPL). The “perplexity of a language model on a test set is the inverse probability of the test set normalized by the number of words.” (Jurafsky and Martin 2025, 39) We calculate the perplexity of a number of different text passages, and use it to assess how familiar the LLMs are with the two philosophers.
Finally, we run our prompting experiments on seven different LLMs of various sizes. This diversity is to allow some generalization of our findings. Most of the LLMs are open-weight, and among the leading models in December 2024. These include Google’s Gemma-2-9B and Gemma-2-27B (Gemma Team et al. 2024), Meta’s Llama-3.1-8B and Llama-3.3-70B (Grattafiori et al. 2024), Alibaba Cloud’s Qwen-2.5-7B and QwQ-32B-preview (Qwen Team 2024), plus the closed source Claude-Sonnet-3.5 by Anthropic (Anthropic 2024). All these LLMs use the transformer architecture, are pre-trained on over 13 trillion tokens (in several languages but mainly English), and have also been further ‘instruction trained.’ QwQ (Qwen with Questions) further describes itself as an “experimental research model focused on advancing AI reasoning capabilities” (Qwen Team 2024b).4 We ran our experiments locally on the ollama5 platform (and the related Python bindings for llama.cpp) using 4-bit quantized models, a temperature of 0.7, and a default system prompt.6
Results
How Familiar Are LLMs with Rawls & Nozick
As discussed in the Methods, we explicitly test the familiarity of the LLMs with the works of Rawls and Nozick using the perplexity metric. For this purpose, we picked a famous and a not-so-famous passage from each of the philosophers.7 Additionally, for comparison, we picked as baseline a sentence that we are sure the models have seen many times, the starting sentence of the United States Declaration of Independence (“We hold these truths to be self-evident [...] and the pursuit of Happiness.”), and a random quote from one of our colleagues.
The results are presented in Table 1. A lower perplexity score indicates the model is less surprised by a text, meaning that it has seen it or similar texts in its training data. The perplexity score can range from 1 to theoretically infinity. First, we can see that across all models, the passage from the US Declaration of Indepence gets a perplexity of close to 1, and the random quote over 100 (as expected). Next, the famous quotes by Rawls and Nozick both score quite low on perplexity, suggesting that the models have been trained on passages from these philosophers (which is good since we can now continue with our main experiments); the less famous passages have a perplexity score between 20 and 50. Finally, a minor observation is that most models seem to be slightly more familiar with Rawls’ than Nozick’s texts, except the Llama-3.3-70B model which seems equally familiar with both texts8.
LLM9 | Perplexity Score | |||||
US Decl. (base-l) | Random (base-h) | Rawls famous | Rawls other | Nozick famous | Nozick other | |
Gemma-2-9B | 1.5 | 208.3 | 4.0 | 45.5 | 13.7 | 35.0 |
Gemma-2-27B | 1.4 | 260.1 | 3.3 | 42.9 | 13.9 | 31.2 |
Llama-3.1-8B | 1.3 | 140.1 | 3.4 | 34.0 | 8.5 | 23.6 |
Llama-3.3-70B | 1.3 | 141.3 | 2.3 | 29.6 | 3.2 | 20.7 |
Comprehension Tests
Our evaluation of the LLMs’ responses to the prompts involved careful reading and interpretation of each reply in terms of three aspects: recall and application of Rawls’ and Nozick’s theories to the novel scenario, and the LLMs’ reflection on their own answers. Table 2 summarizes this evaluation, indicating whether each model performed well regarding these three aspects, with comments detailing and justifying our assessment.
LLM | Size | Training | Prompt | Recall | Application | Reflection10 | Notes |
Gemma2-9B | 9B | Distilled from Gemma-2-27B | Rawls | x | x | - | Has some minor errors, e.g. recalls Nozick’s ideas but not the entitlement theory |
Nozick | x | x | - | ||||
Gemma2-27B | 27B | 13T tokens +instruct | Rawls | x | x | - | Surprisingly, while the recall is bad for Nozick, the application of the theory remains correct |
Nozick | ? | x | - | ||||
Llama 3.1-8B | 8B | 15.6T tokens +instruct | Rawls | x | x | - | Appears to misinterpret the prompt (Fail) |
Nozick | - | - | - | ||||
Llama 3.3-70B | 70B | 15.6T tokens +instruct | Rawls | x | x | - | Very generic responses with limited relation to Rawls’ or Nozick’s theory. |
Nozick | x | - | - | ||||
Qwen2.5-7B | 7B | 18T tokens + instruct | Rawls | x | ? | - | Misinterprets the prompt; some proposed solutions not related to Rawls’ theory. Confuses Nozick’s and Rawls’ theories, making the answer incorrect. (Fail) |
Nozick | - | - | - | ||||
QwQ-32B-preview | 32B | 18T tokens +instruct +reasoning | Rawls | x | x | x | Original and creative answers in both cases, even more for Nozick. |
Nozick | x | x | x | ||||
Claude-Sonnet-3.5 | >100B11 | undisclosed | Rawls | x | - | - | Answers are overly formulaic (bullet points) with no reflection. In Rawls’ case, the application does not consist of specifically Rawlsian proposals. |
Nozick | x | x | - |
The evaluation revealed significant variations in LLMs’ ability to produce responses that engage with Rawls’ and Nozick’s theories across the levels of Bloom’s taxonomy. Among the seven models assessed, QwQ-32B’s output demonstrated the highest level of comprehension, accurately recalling principles of the two respective theories, applying them to the new scenario, and offering reflection on its own response. The model performed best while responding to prompts on both philosophers, with a slightly weaker answer in the Rawls’ case.
To illustrate, QwQ-32B’s response first recalled the title of A Theory of Justice and identified the main elements of the theory—such as the original position and veil of ignorance. The model then went on to explain that the Rawls’ “main idea is that a just society should be structured in a way that benefits the least advantaged members the most.” It then explained how the theory relates to the new scenario: “In this geometric shapes world, the shapes don’t choose their number of angles; it's assigned at creation. So, the number of angles is like a natural attribute, similar to talents or abilities in the real world.” While applying it to the scenario, the response offered nuanced and reflective reasoning, first by stating that “to apply Rawls’s theory, we need to design a system where the shapes with more angles are compensated or supported in some way to ensure that the overall distribution of advantages is as fair as possible” and then by reconsidering the proposed solution:
“But wait, in Rawls's difference principle, it’s not just about helping the least advantaged, but also allowing inequalities to exist if and only if they benefit the least advantaged. So, perhaps some advantages for shapes with fewer angles could be permitted if those advantages trickle down and help the shapes with more angles as well.
For example, maybe the Highest Council, composed mostly of shapes with fewer angles, implements policies that specifically benefit shapes with more angles. So, even though it’s easier for triangles and squares to get into the council, once they’re there, they make decisions that improve the lives of pentagons, hexagons, etc.”
After further reflection, it offered an even more unexpected and creative solution: “Wait a minute, perhaps the number of angles affects their abilities in specific ways. For instance, triangles might be more mobile or flexible, while pentagons or hexagons might be more stable or have better structural integrity. So, depending on what the Highest Council needs to do, different shapes might have different advantages.”
The same model, QwQ-32B, generated a similarly creative response to the prompt about Nozick’s theory. The response consisted of a correct recall of the elements of entitlement theory and application to the novel scenario. The text then presented a lengthy, reflective analysis, with argumentation not only considering different ways of addressing the scenario with the use of Nozick’s concepts, but also questioning its own responses and admitting some puzzlement over the implications of the reasoning:
“In this case, since shapes don't choose their angles, and assuming that the angle count doesn't reflect any moral or merit-based characteristic, perhaps Nozick would argue that measures should be taken to ensure that all shapes have equal basic liberties and opportunities, without necessarily eliminating the advantages based on angle count.
Alternatively, he might argue that as long as no shape is being coerced or disadvantaged in a way that violates their rights, the system is just, even if it leads to unequal representation in the council.
I'm a bit stuck here because Nozick’s theory is more about the justice of holdings and transactions rather than about social justice or equality of opportunity in the way that John Rawls might discuss.”
Eventually, it generated its final answer: “According to Nozick’s theory, the system is just if the initial acquisition of angle counts was just, transfers are voluntary and just, there are no coerced transactions or rights violations, and the Highest Council protects the rights of all shapes without favoritism.”
In contrast, Qwen2.5-7B’s response offered, in the case of Rawls’ theory, a more limited recall of the principles of justice and no mention of “original position” or “veil of ignorance.” By misunderstanding the scenario—in the generated text it was assumed that shapes with fewer angles would be more disadvantaged—it attempted to apply the two principles but without much nuance or in-depth comprehension of Rawls. The proposed solution was characterized by the focus on interaction which is not stressed in the Rawlsian conceptual framework:
“Inclusivity and Fairness in Interaction: Establish clear rules for interactions among shapes to prevent discrimination based on the number of angles. For instance, interaction protocols should ensure that all shapes can communicate effectively and engage in meaningful relationships without prejudice.”
This model performed even worse on the level of recall while considering Nozick’s theory by conflating it with Rawls’ principles: “To address this question through the lens of Robert Nozick’s theory of justice as fairness, we need to consider his key principles: the difference principle and the entitlement principle”. In consequence, the proposed solution to the scenario was a confusing mixture of the two theories.
A similarly bad response was given by Llama-3.1-8B for Nozick’s theory. Even though the generated text recalled the title of “Anarchy, State, and Utopia,” it identified the maximin principle as Nozick’s principle of distributive justice, even though it is used in political philosophy in reference to Rawls’ difference principle—as it aims at maximizing the welfare of people at the society’s minimum level. The same model performed only slightly better answering the scenario using Rawls’ theory, but similarly to the smaller Qwen model, it misinterpreted the prompt and assumed that the lower number of angles is associated with lower advantage, thus offering this solution: “Shapes with fewer angles could have priority access to coveted spaces or positions within the society.”
Even the larger of Meta’s models, Llama-3.3-70B, gave a confused answer with regards to Nozick. In its response, it correctly included protection of individual rights, but then went on to explain and apply the concept of non-discrimination which is not a part of Nozick’s vocabulary. It then recalled the Lockean proviso, which is part of Nozick’s conceptual framework, but offered its incorrect interpretation:
“Lockean proviso: Ensure that the benefits of being part of the Highest Council are not solely reserved for shapes with fewer angles, but rather that all shapes can benefit from the council’s decisions and actions in some way.”
Some LLMs–in particular Llama 3.3-70B and Claude Sonnet 3.5—offered not necessarily completely erroneous, but frequently more generic replies. These replies referenced some of the ideas associated with ideologies represented by Rawls or Nozick, i.e., either egalitarian or libertarian, but which are not explicitly endorsed by these philosophers.
It must be noted that evaluation of the responses is always in part based on one’s reactions to the rhetoric and structure of the reply. A conversational response may convey an impression of a more human-like, reflective thought-process behind the answer. This is especially important in the context of assessing the ability to justify their own reasoning (which relates to higher Bloom levels), and it appears that the reasoning model acts in this way by default. Similarly, a reply consisting of bullet points instead of paragraph text could be taken as drier and more generic. Admittedly, these properties of LLMs’ responses could be changed by asking a follow-up question or reframing the original prompt, for example by requesting the model to assume a student’s persona.
Returning to our research question on whether LLMs can map distinctive ideologies to a novel scenario in a convincing manner, we can state that the answer depends on the LLM and philosopher, and for at least one of the models we tested (among seven) the answer is an astounding yes. The LLMs as a whole struggled more with applying Nozick’s theory as compared to Rawls, which probably relates to the fact that Rawls is better known (and thus more highly cited). In a few strange cases, typically for the smaller models, a bad recall was followed by a correct application. This on the one hand points to a limitation of the hierarchical structuring of Bloom’s taxonomy. But it might also be suggesting that smaller models have less capacity to memorize all kinds of texts, while still having “learned” the concept enough to be able to generalize it12.
Discussion
The aim of this paper was to demonstrate that LLMs can comprehend political ideologies beyond surface-level patterns (that is a lookup table of word/token frequencies). We set up an experiment involving applying theories to a novel scenario, with the obvious idea that a correct answer couldn’t have been simply memorized and thus would indicate some level of ‘transfer’ (and hence comprehension)13. In other words, we argue that our preliminary analysis establishes at least that LLMs generate responses suggesting they are more than just “stochastic parrots” (that is replicating previously learned data). Nonetheless, one could still speculate that some elements of the prompt, such as the names of the philosophers, or words describing the relationship between imaginary entities (e.g., “less angles”), activate parts of the neural network that consist of similarly structured sentences, allowing the LLM to generate plausible responses. In other words, the fact that the LLM discusses geometric shapes and not human beings remains incidental. However, in our opinion this cannot explain the more creative and deeper parts of the responses (e.g. by the “Qwen with Questions” model). Educators certainly consider the ability of a student to reflect and justify one’s opinions as a sign of sufficient understanding.
A clear limitation of our exploratory analysis is that we analyzed outputs of models to look for evidence that implies existence of internal world models (as networks of concepts). The necessary next step would be to complement this paper with probes of internal representations within the models. Such an analysis should focus on features, which are defined as fundamental units of neural networks, and can form circuits consisting of interconnected patterns of activations (Olah et al. 2020). Such an approach could try to locate the political concepts that would be found within a morphological analysis of the ideologies. This is not to say that the mechanisms that allow humans to understand the world through ideological concepts are the same as the mechanisms that allow LLMs to generate well-justified text (although similarities might well exist). It is rather to suggest that the morphological analysis of ideologies could be a substantive reference for studying structures of meaning embedded in neural networks.
Another critique of our work could be that using Bloom’s taxonomy to evaluate LLM responses perpetuates the use of language that anthropomorphizes AI. While we acknowledge that the use of anthropomorphic language is frequently unhelpful (Placani 2024), we also need to stress that the use of terms such as creativity to describe and evaluate LLMs’ outputs does not necessarily mean that we blur the boundaries between humans and machines. As suggested by Boden (Boden 2004), creativity, defined as “ability to come up with ideas or artefacts that are new, surprising and valuable” could be applied to both human and artificial intelligence alike. We would still agree that we might need new terminological frameworks to help evaluate comprehension of LLMs’ outputs without assigning to them human characteristics. However, to reiterate, our analysis primarily explores whether LLMs might utilize conceptual maps/networks that allow them to produce meaningful responses beyond “autocomplete”, not whether LLMs reason or understand like humans.
In closing, we want to point out the benefits of our research to political theorists. The field of political theory remains an interpretive one, being traditionally less engaged with computational methods, relying instead on conceptual and contextual analysis that links it to both philosophy and history of ideas. While we are not suggesting that this kind of theoretical reflection be replaced by the use of LLMs, our research suggests a way to bridge the interpretative analysis of ideologies and computational methodologies. The fact that the LLMs demonstrate capabilities to apply complex theories and concepts and reason about their possible implications could be interesting for political theorists attempting to understand the consequences of particular ideological propositions. The models that exhibit some degree of creativity in that regard could then augment the conceptual analysis. A closer collaboration between computer scientists and political theorists could help reveal and explain other properties of LLMs and enrich the methodologies of both fields.